Coefficient Of Dispersion
The coefficient of dispersion is how municipalities can determine differences between the assessed values of properties in an area or neighborhood. It gives a broader look at the state of the market, and a way to evaluate how consistent the appraisal of the properties is. The definition of the coefficient of dispersion that is used exclusively in dealing with market values and properties is a measure of how much values of a particular variable vary around the mean or median. The end value is represented in percentage from the median.
The Coefficient of Dispersion’s formula:
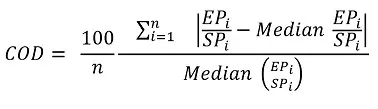
COD = coefficient of dispersion
N = number of properties in the sample
EPi = appraised value of ith property
SPi = sale value of ith property
∑ = summation of all the values in the group
How to Calculate the Coefficient of Dispersion?
After that insane formula, we understand if homeowners want to stay clear of it, but there are reasons why any homeowner would want to use it. If, for example, you’re house was appraised at a value that is higher than you expect, and the same happened to other neighbors, you can figure out if this is a trend in the area to increase taxes or just the increase of the market value in the area.
Example:
John investigated and managed to find the appraised value of 7 properties around him as well as the actual price for those properties.
|
Appraised Value |
Sales Price |
|
359,000 |
370,000 |
|
362,000 |
373,000 |
|
347,000 |
358,000 |
|
329,000 |
340,000 |
|
384,000 |
396,000 |
|
372,000 |
386,000 |
|
395,000 |
396,000 |
Now, John finds out the median appraised value by adding all the appraised values, then dividing it by seven properties ($362,000) and does the same to the median sale price ($373,000). With these values, he can start using the formula.
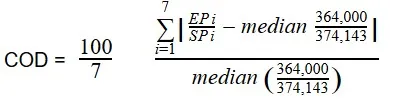
The median appraised value divided by the median sale value is 0.9729.
John returns to his table to discover the EPi/SPi for each property because the ∑ requires him to discover that value independently for each before he subtracts 0.9729 (the median EPi/SPi) from each:
|
Appraised Value |
Sales Price |
EPi/SPi |
|
359,000 |
370,000 |
0.9702 |
|
362,000 |
373,000 |
0.9705 |
|
347,000 |
358,000 |
0.9692 |
|
329,000 |
340,000 |
0.9676 |
|
384,000 |
396,000 |
0.9696 |
|
372,000 |
386,000 |
0.9637 |
|
395,000 |
396,000 |
0.9974 |
With that out of the way, John needs to subtract 0.9729 from each value. Here he considered negative values positive:
|
Appraised Value |
Sales Price |
EPi/SPi |
EPi/SPi-0.9729 |
|
359,000 |
370,000 |
0.9702 |
0.0027 |
|
362,000 |
373,000 |
0.9705 |
0.0024 |
|
347,000 |
358,000 |
0.9692 |
0.0037 |
|
329,000 |
340,000 |
0.9676 |
0.0053 |
|
384,000 |
396,000 |
0.9696 |
0.0033 |
|
372,000 |
386,000 |
0.9637 |
0.0092 |
|
395,000 |
396,000 |
0.9974 |
0.0245 |
Now that he has all the data necessary, John can work the formula:
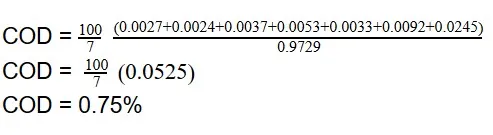
The coefficient of dispersion is a complex formula but the example above tells us that the average difference the houses have from the median of the assessed sales ratio is 0.75%.
Popular Real Estate Terms
Number of range grassland acres needed to support one animal unit for a specified period of time or grazing season. ...
Commercial building having several different uses blending together. For example, retail shops are on the first floor, professional offices are on floors two through ten, and a restaurant ...
The term assessed value is used to define the dollar value of a property for the applicable taxes. The evaluator, a tax assessor, determines the property’s assessed value for tax ...
Equals the tax divided by taxable income. Foe example, if the tax is $30,000 on taxable income of $120,000 the effective tax rate if the business is 25% ($30,000/$120,000) ...
Market condition in which sellers exceed buyers, thereby causing prices to fall. In real estate, declining markets may result from unfavorable business conditions and high interest rates. ...
Unequal treatment and denial of opportunity to individuals based on race, color, creed, nationality, age, or sex. The Civil Rights Acts passed by the U.S. Congress included those of 1866, ...
First right of a party, usually a creditor, to hold, keep possession of, or control the property of another to pay a debt, duty, or obligation. ...
Claim on property by an unpaid workman or contractor. The property may be sold to recover the money owed. The legal justification of the mechanic's lien is that the labor and materials ...
You can frequently encounter “circa” in everyday discourse, referring to an approximation as an approximate date. Variations of circa are: about, near, and roughly. The ...
Comments for Coefficient Of Dispersion
COD example unclear
Jan 15, 2023 09:18:18Hello. Let us shed some light on this.
Someone wants to find out the appraised value of several properties around them. and the sale price is higher. Then they discover the median appraised value ($362,000). They add all the appraised values of all the properties and divide them by the number of properties. And later does the same with the median sale price ($373,000) The median appraised value divided by the median sale value is around 0.9. Then, they calculate that the average difference between houses and the median is 0.75.
Jan 20, 2023 09:22:24Have a question or comment?
We're here to help.